Graph These Data and Draw the Least Squares Line
Hands-on Tutorials
Partial Least Squares
A deep-dive into Partial Least Squares Regression and Partial Least Squares Discriminant Analysis with full worked-out examples in R and Python
![]()

Partial Least Squares
In this article, you'll discover everything you need to know about Partial Least Squares. As the name indicates, Partial Least Squares is related to Ordinary Least Squares: the standard mathematical approach for fitting a Linear Regression.
Partial Least Squares against multicollinearity
The goal of Linear Regression is to model the dependence relationship between one dependent (target) variable and multiple independent (explanatory) variables. Ordinary Least Squares works great for this, as long as you meet the assumptions of Linear Regression.
In some domains, it may ha p pen that you have a lot of independent variables in your model, of which many are correlated with other independent variables. If this happens, you can get into trouble if you use OLS: you will have multicollinearity and therefore violate the assumptions of Linear Regression.
Partial Least Squares is a solution for this case: it allows you to reduce the dimensionality of correlated variables and model the underlying, shared, information of those variables (in both dependent and independent variables).
Partial Least Squares for multivariate outcome
A second large advantage of Partial Least Squares is that it is a method that can model multiple outcome variables. Many statistics and Machine Learning models cannot deal directly with multiple outcome variables.
Solutions can often be found for those models. For instance, building one model per variable. Yet especially for analytical use cases, it can be essential to keep everything in one model, as the interpretation of one multivariate model will be different from the interpretation of many univariate models.
Partial Least Squares versus other models
You have just seen that there are two main reasons to use Partial Least Squares: having multiple dependent variables and having many correlated (independent) variables.
There are other methods that propose solutions for those problems. Before getting into the details of Partial Least Squares, let's see a few of the competing methodologies.
Partial Least Squares vs Multivariate Multiple Regression
Multivariate Multiple Regression is the multivariate counterpart of Multiple Regression: it models multiple independent variables to explain multiple dependent variables.
Although Multivariate Multiple Regression works fine in many cases, it cannot handle multicollinearity. If your dataset has many correlated predictor variables, you will need to move to Partial Least Squares Regression.
Partial Least Squares vs Principal Components Regression
Principal Components Regression is a regression method that proposes an alternative solution to having many correlated independent variables. PCR applies a Principal Components Analysis to the independent variables before entering them into an Ordinary Least Squares model.
PCR can be done in two steps, by doing a PCA followed by a Linear Regression, but there are also implementations that do both steps at once.
The difference between Partial Least Squares and Principal Components Regression is that Principal Components Regression focuses on variance while reducing dimensionality. Partial Least Squares on the other hand focuses on covariance while reducing dimensionality.
In Partial Least Squares, the identified components of the independent variables while be defined as to be related to the identified components of the dependent variables. In Principal Components Regression, the components are created without taking the dependent variables into account.
When the goal is to find a dependence relation between dependent and independent variables, Partial Least Squares has an advantage here.
Partial Least Squares vs Canonical Correlation Analysis
Canonical Correlation Analysis is a statistical method that focuses on studying the correlation between two datasets. This is obtained by a reduction of dimensionality on both of the datasets and find the pairs of components that have the maximum amount of correlation.
The idea is between Partial Least Squares and Canonical Correlation Analysis is quite comparable. The main difference between the methods is that Partial Least Squares focuses on covariance, whereas Canonical Correlation Analysis focuses on correlation.
PLS models
Now that we've seen the general reasons to use Partial Least Squares, let's go into a bit more detail.
Within Partial Least Squares, there are subcategories, and the literature on PLS is full of confusing terms and categories. Before going into the implementation of an example, let's try to clarify some of the terms that you'll run into when learning about PLS and give a list of the different PLS models.
Partial Least Squares Regression
The absolute most common Partial Least Squares model is Partial Least Squares Regression, or PLS Regression. Partial Least Squares Regression is the foundation of the other models in the family of PLS models. As it is a regression model, it applies when your dependent variables are numeric.
Partial Least Squares Discriminant Analysis
Partial Least Squares Discriminant Analysis, or PLS-DA, is the alternative to use when your dependent variables are categorical. Discriminant Analysis is a classification algorithm and PLS-DA adds the dimension reduction part to it.
PLS1 vs PLS2
In some literature and software implementations, a distinction is made between PLS1 and PLS2. PLS1 in this case refers to a Partial Least Squares model with only one dependent variable, whereas PLS2 refers to a model with multiple dependent variables.
SIMPLS vs NIPALS
SIMPLS and NIPALS are two methods for doing PLS. SIMPLS was invented as a faster and 'simpler' alternative to the earlier version NIPALS. When executing a PLS, it is probably not that important, as the results from both methods will be quite close. Yet, if you can choose, it'd probably be best to go with the more modern SIMPLS.
KernelPLS
Partial Least Squares, as said before, is a variation on Ordinary Least Squares (Linear Regression). Because of this, Partial Least Squares cannot be applied to nonlinear problems. Kernel PLS solves this problem and makes Partial Least Squares available for nonlinear problems. Kernel PLS fits a relationship between input and output variables in a high-dimensional space so that the input data set can be considered linear.
OPLS
OPLS, short for Orthogonal Projects to Latent Structures, has been proposed as an improvement of the Partial Least Squares method. OPLS promises to be easier to interpret. There where PLS only splits variability into systemic and noise, the OPLS goes a step further by splitting systemic variability into predictive and orthogonal variability.
There are also some critics on OPLS as both methods are known to obtain the same predictive performance (we could consider that it is not a 'real' improvement if it doesn't yield better performance) and, secondly, traditional PLS is faster.
For the rest of this article, we'll stick with traditional PLS as it's simpler to execute and just as performant.
SPLS
SPLS, short for Sparse Partial Least Squares, is a variation on the PLS model. As stated earlier, PLS has as an objective to do dimension reduction: reducing a large number of correlated variables into a smaller number of components.
The goal of SPLS is to do more than just dimension reduction. In addition, it also applies variable selection. SPLS uses the famous LASSO penalization to do variable selection in both the X and Y data sets, with the goal of obtaining components that are easier to interpret.
L-PLS
L-PLS is a proposed variation on PLS that can be applied for some specific use cases. The method was proposed by Martens et al in 2005:
A new approach is described, for extracting and visualising structures in a data matrix Y in light of additional information BOTH about the ROWS in Y, given in matrix X, AND about the COLUMNS in Y, given in matrix Z. The three matrices Z–Y–X may be envisioned as an "L-shape"; X(I × K) and Z(J × L) share no matrix size dimension, but are connected via Y(I × J ).
As they describe it in their article, the idea behind L-PLS is to use three data sets for one and the same regression problem, so that you have additional data on the rows and on the columns. They describe this situation as having data in the form of an L and this is represented by the L in L-PLS.
This method is very innovative and there are certainly use cases for it. Unfortunately, the lack of implementation in popular statistics libraries and its highly specific application make that it is not much used in practice yet.
Partial Least Squares Regression Example
In this example, we will use the meats dataset. As requested by the publishers of this dataset, here is the official notice that comes with the data:
Fat, water and protein content of meat samples
"These data are recorded on a Tecator Infratec Food and Feed Analyzer working in the wavelength range 850 - 1050 nm by the Near Infrared Transmission (NIT) principle. Each sample contains finely chopped pure meat with different moisture, fat and protein contents. If results from these data are used in a publication we want you to mention the instrument and company name (Tecator) in the publication. In addition, please send a preprint of your article to Karin Thente, Tecator AB, Box 70, S-263 21 Hoganas, Sweden
The data are available in the public domain with no responsibility from the original data source. The data can be redistributed as long as this permission note is attached."
"For each meat sample the data consists of a 100 channel spectrum of
absorbances and the contents of moisture (water), fat and protein. The absorbance is -log10 of the transmittance measured by the spectrometer. The three contents, measured in percent, are determined by analytic chemistry." Included here are the traning, monitoring and test sets.
The goal of the meats data is to take 100 automated Near-Infrared measurements of meat and use them to predict the water, fat, and protein contents of the meat. This example has multiple reasons to use Partial Least Squares:
- It has many independent variables that could be correlated. At least they are very un-interpretable which is a great case for doing a dimension reduction on them.
- There are multiple dependent variables, that also may have some correlation between them.
The goal of such a model would be to be able to infer Fat, Water, and Protein content of meat directly from chemometric measurements. So basically the ideal goal would be to make you able to avoid doing time-consuming measurement work and just put your meat in the scanner and obtain the estimated Fat, Water, and Protein content.
This use case, like most chemometric use cases for Partial Least Squares, is mostly focused on obtaining the best possible performance. Analysis and interpretation of the model are secondary. We'll see a second example later on in which interpretation is central rather than predictive performance.
When doing models for predictive performance, it is always important to do a model benchmark with different models. You can refer to this Machine Learning starter guide for ideas on how to go about such benchmarking set-ups, or check out this article on Grid Search: a great method for model tuning.
Partial Least Squares Regression R
To get started, let's import the data in R. The data are present in the modeldata library, so you can use the following code to import the data:
The data looks as follows: 100 columns with chemometrics measures and three columns that give the measures of water, fat, and protein content:
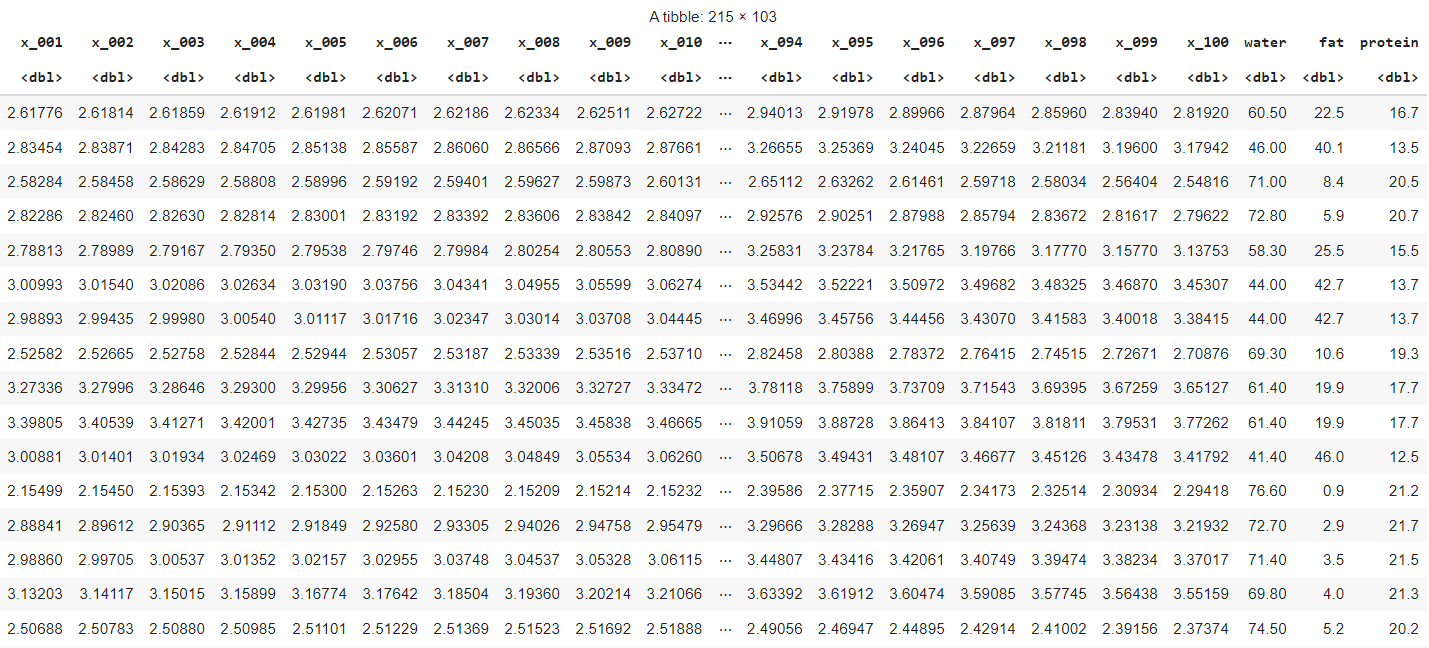
As said before, we will try to build a PLS Regression model that can predict water, fat, and protein content from the 100 measurements. In order to do this, we want to be certain of obtaining predictive performance out-of-sample rather than explaining a maximum within-sample variation.
To obtain this, we'll split the data into three datasets:
- train data for training the model
- validation data for tuning the model
- test data for having a final estimate of out-of-sample error
Generally, it's best to do a random split of your data. However, to make the example easier to follow along, you can do a non-random split of the data as follows:
The next step is to fit a full model. That is, a model with the maximum number of components:
Now that we have the most complex model, we'll use it to identify which number of components we should use to obtain the best predictive performance: a non-trivial decision.
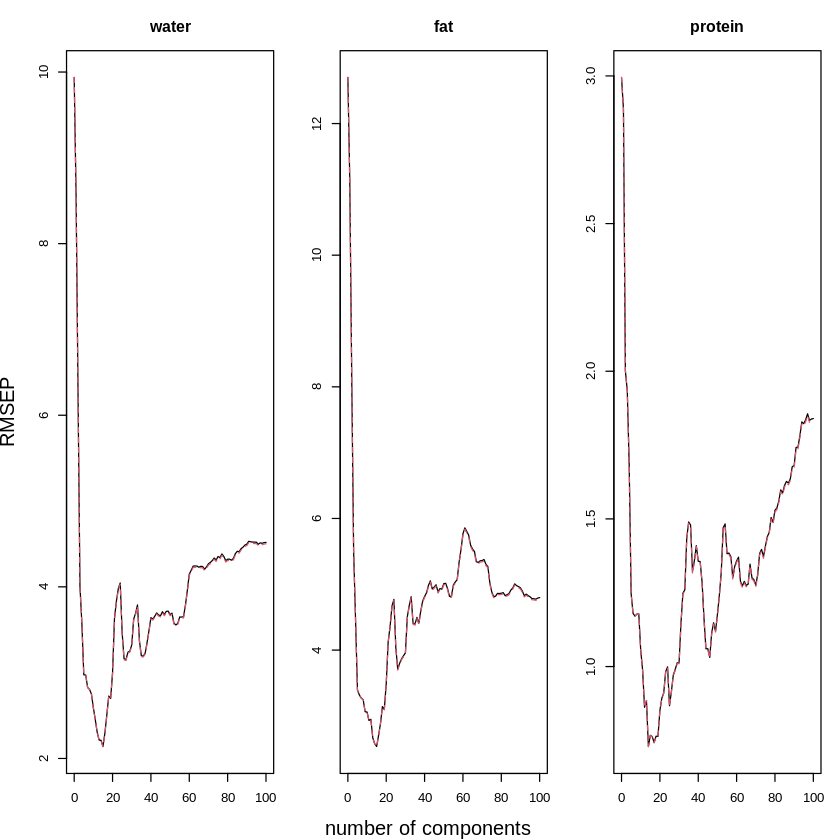
A first thing we can look at is the plot of the Root Mean Square Error of Prediction for each number of components and each dependent variable. In this R function, the built-in Leave-One-Out Cross-Validation function is used:
You will obtain the following three plots to show that the predictive error (opposite of predictive performance) is highest in a model with a very low number of components, then gradually decreases and when models have too many components they again have high errors.
The best value should be between 15 and 20.
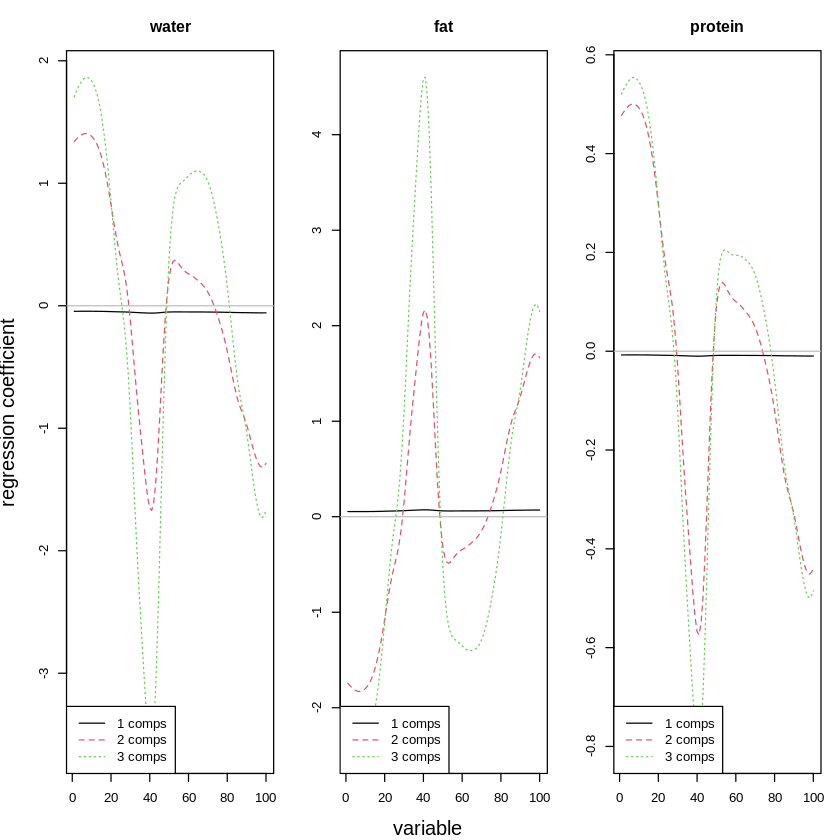
To understand better what happens when having more or fewer components, we can check the following graph. It shows the regression coefficients for each of the variables (each corresponds to a wavelength).
The plot clearly shows that the more components we use, the more difficult the patterns become:
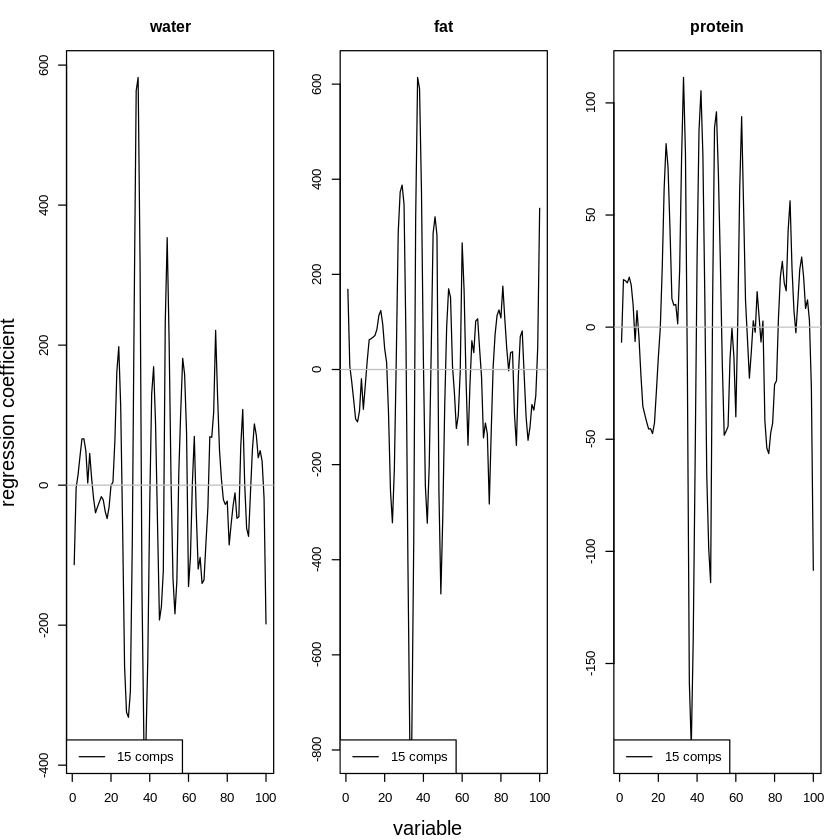
For comparison, a mode with fifteen components is even much more complex:
This complexity can be seen in the following graph, as coefficients are much more extreme (some much lower, some much higher):
Now, these graphs are great to obtain estimates for the best number of components. Yet it would be much more practical to obtain a fixed number as an output. Grid Search is a tool that allows you to search a grid of values for the best predictive performance. It is often used for tuning hyperparameters for ML models and we'll use it here to tune the ncomp hyperparameter:
This obtains a best_r2 of 0.9483937 for a best_ncomp of 19. This means that the PLS Regression model with 19 components is, according to the Grid Search, the best model for predicting water, fat, and protein content of meats.
As a final check, let's verify if we also obtain a good score on the test data set using the following code:
The best model obtains a predictive average R2 score of 0.9726439. We now have successfully tuned the PLS Regression model for the use case of predicting water, fat, and protein content. If this margin of error is acceptable for the precision needed in measurements of meat, we can replace handmade measurements with automated chemometrics measurements. We can then use the PLS Regression model to convert those automated measurements into estimates of water, fat, and protein content.
Partial Least Squares Regression Python
For those who prefer Python, let's also do an implementation in Python before moving on to the categorical data example.
In Python, you can import the meats data from my S3 bucket where I stored a copy of the data from R. Please note the disclaimer that comes with the data higher in this article.
The data in Python will look as follows:
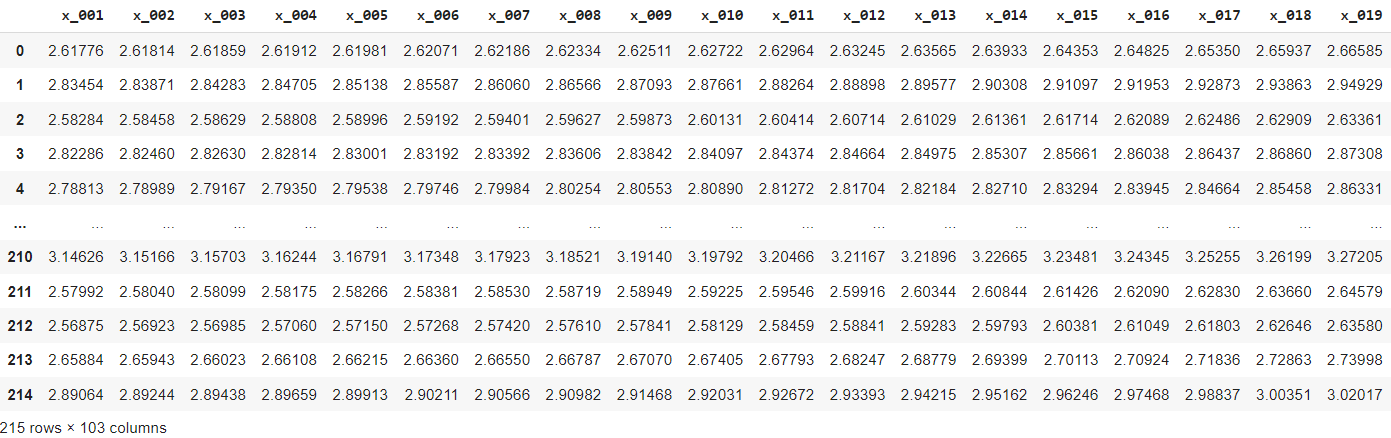
To obtain the same non-random split of train, validation, and test data as the one in R, you can use the code below. You can also go for a random sample using scikitlearn's train_test_split function if you don't mind having slightly different outcomes.
Now, the complete model can be estimated as follows:
Just like we did in R, you need to tune the number of components. The plot of predictive error as a function of the number of components can be created as follows:
It will give you the following graphs that show an optimal number of components somewhere in the range of 15 to 20.

Now, it can be nice to visualize the differences in results for different numbers of components. As there are 100 coefficients in the model, the numerical data is hard to look at. The following plot shows the coefficients in a plot:
The plot looks as follows for the three dependent variables from left to right (water, fat, protein) and the number of components ( 1=blue, 2=orange, 3=green).

You can see that the model becomes more complex with more components involved, just like we saw with the R code.
Now, let's move on to the Grid Search to find the best value for n_comp , the number of components. We compute an R2 score on the validation data for each of the possible values of n_comp as follows:
The best R2 that we can obtain is an R2 score of 0.9431952353094432 with a value of ncomp at 15.
As a final validation of our model, let's verify if we obtain a comparable score on the test data set:
The obtained R2 score is 0.95628, which is even slightly higher than the validation error. We can be confident that the model does not overfit and that we have found the right number of components to make a performant model.
If this error is acceptable for meat testing purposes, we could confidently replace hand-made measurements of water, fat, and protein with the automated chemometrics measurements in combination with this PLS Regression. The PLS Regression would then serve to convert chemometrics measurements into estimations of water, fat, and protein contents.
Partial Least Squares Discriminant Analysis Example
For this second example, we'll be doing an explanatory model: a model that focuses on understanding and interpreting the components rather than obtaining predictive performance.
The data is a data set on olive oil. The goal is to see if we can predict the country of origin based on chemical measurements and sensory measurements. This model will allow us to understand how to differentiate olive oils from different countries based on chemical and sensory measurements.
The dependent variable (country of origin) is categorical, which makes it a great case for Discriminant Analysis because this is a method in the family of classification models.
Partial Least Squares Discriminant Analysis R
In R, you can obtain the Olive Oil data set as soon as you import the pls library. You can do this as follows:
The data looks as follows. It contains two matrices: a chemical matric with 5 variables of chemical measurements and a sensory matrix with 6 variables of sensory measurements:
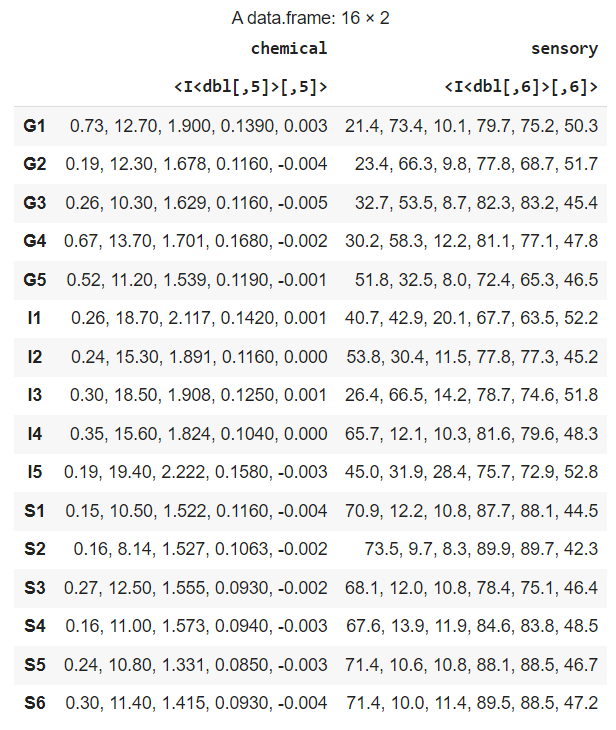
Of course, this data format is not ideal for our use case, so we need to make the data frame of two matrices into just one matrix. You can do this as follows:
The resulting matrix looks like this. As you can see it automatically contains the column names:
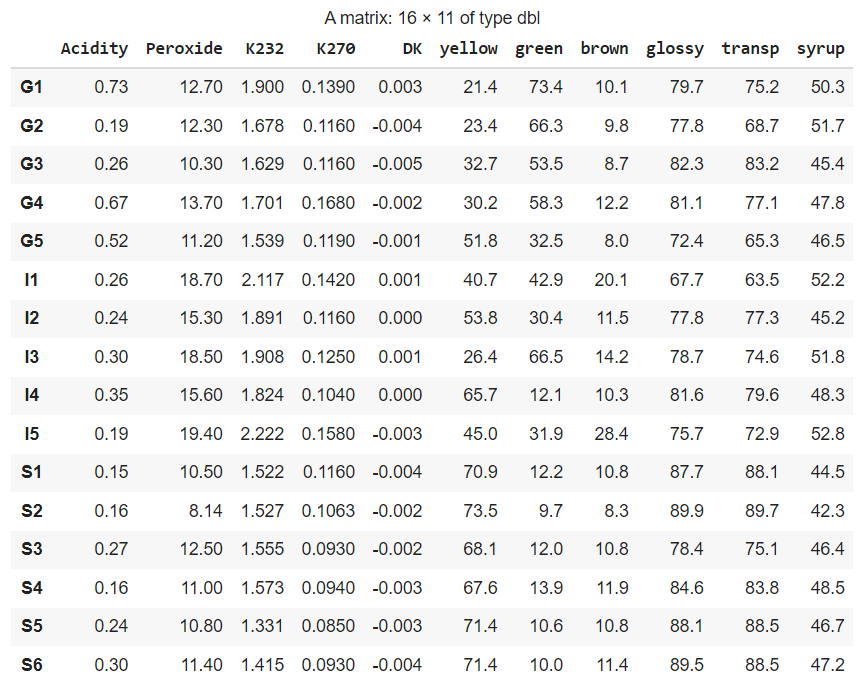
The country is the first letter of the rownames (G for Greece, I for Italy, and S for Spain). Here is an easy way to create the Y data as a factor. Factors are categorical data variables in R.
Now, we get to the model. We will use the caret library for fitting the model. Caret is a great library that contains lots of Machine Learning models and also a lot of tools for model development. If you're interested in caret, you could check out this article that compares R's caret against Python's scikit-learn.
You can use the PLSDA function in caret to fit the model, as shown below:
The next step is to obtain the biplot so that we can interpret the meanings of the components and analyze the placement of the individuals at the same time.
To interpret the biplot, you need to look at directions. To understand what this means, try to draw an imaginary line from the middle of the graph to each label. The angle between the imaginary lines is what makes two items close. The distance from the middle makes that weights are strong or weak.
Tip: You could quickly scroll down to the Python biplot to understand the idea of the imaginary lines better!
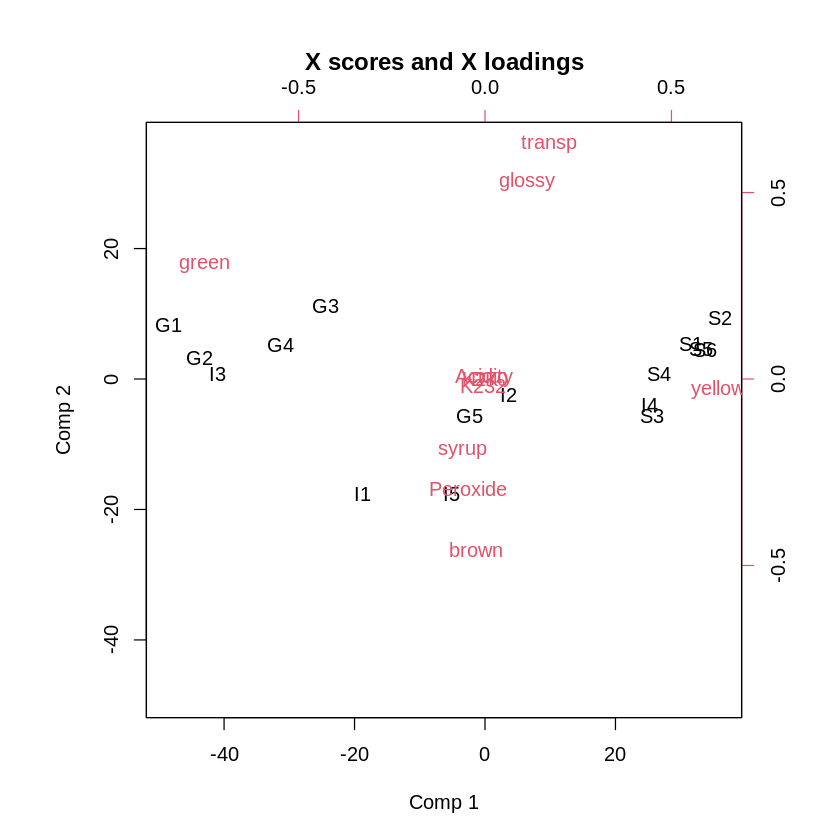
Interpreting the Partial Least Squares Biplot
When using Partial Least Squares for explanatory use cases, a lot can be concluded from the biplot. To keep things simple, we sometimes look at more than two dimensions, but things can quickly get complicated from the third dimension onward. Let's stick to two dimensions here.
- Interpreting the first dimension
The first question that we generally ask ourselves is about the meaning and interpretation of the first dimension. We can define this by looking at the variables (red labels on the plot) that are strongly related to the first dimension. To see those, we can take a variable far on the left (low score on comp 1) and a variable far on the right (high score on comp 1).
In our case, the first component goes from green on the left to yellow on the right. Apparently, the split between green and yellow is important in olive oil!
To confirm this, let's now look at whether there is a trend in individuals (black labels on the plot). We see a lot of Greek oils on the left, whereas we see a lot of Spanish oils on the right. This means that the split between Yellow and Green olive oils allows us to distinguish between Greek and Spanish olive oils!
An interesting insight in terms of variables is that there apparently seems to be a very prominent color gradient in olive oils from yellow to green, whereas brown is not represented by the first dimension.
2. Interpreting the second dimension
Now, let's see what we can learn from the second dimension. First, let's find some representative variables. To do this, we need to find variables that score very high or very low on dimension 2.
We can see that dimension 2 goes from brown on the bottom to glossy and transparent on the top. Apparently, there is an important gradient in olive oils with brown oils on one end and glossy and transparent ones on the other side.
To obtain a learning in terms of countries, let's see how the individuals are distributed along the axis of dimension 2. The split is less obvious than the one from dimension 1. Yet when looking carefully, we can clearly see that italian olive oils are generally browner than other oils. Non-Italian olive oils are also generally more glossy and transparent than the other oils.
An interesting insight in terms of variables is that there is no gradient from brown to another color, but rather from brown on one side to glossy and transparent on the other side. Of course, in reality, an olive oil expert would collaborate on such a study to help interpret the findings.
3. Interpretation of the types of variables in the main components
What we have seen here are the dimensions that are defined as most important by the model. We can note that the most important components mostly exist of sensory components. This means that sensory characteristics seem to work well for detecting the source country of an olive oil. This is also a very interesting learning!
Partial Least Squares Discriminant Analysis Python
The Olive Oil data set is built-in in the R PLS library. I have put a copy on my S3 bucket to make it also easy to import with Python. (Please see the notice for this data set higher up in case you want to distribute it somewhere else).
You can import the data into Python using the following code:
The data looks like this. I have added the countries as a variable, which is not the case in the original R dataset.
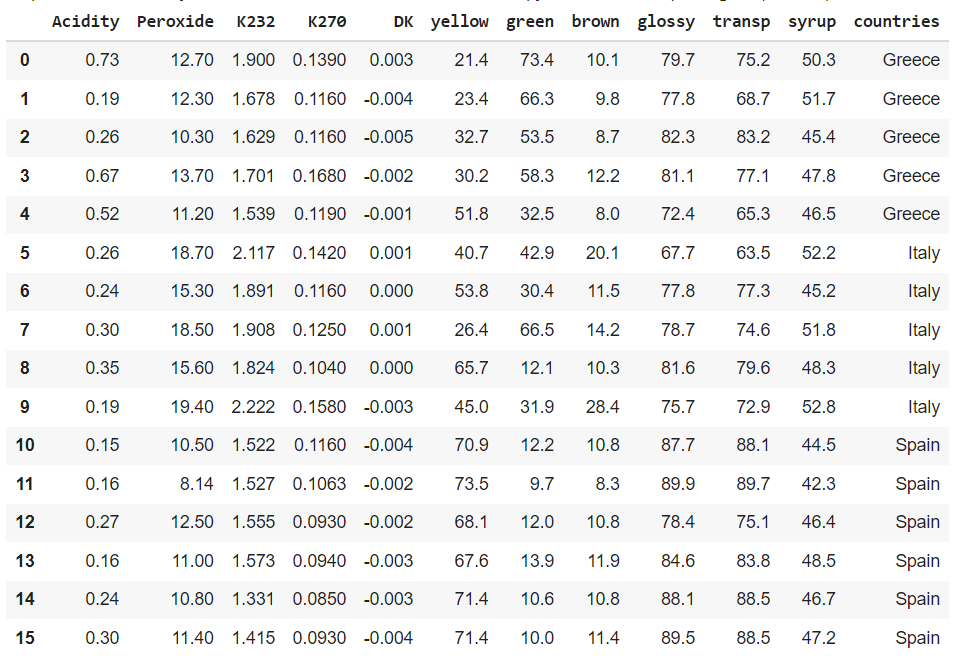
PLS Discriminant analysis in Python is actually done by doing a PLS Regression on a categorical variable that is transformed into a dummy. Dummies transform a categorical variable into a variable for each category with 1 and 0 values: 1 if the row belongs to this category and 0 otherwise.
Dummy encoding is done because 0 and 1's are much easier to use in many Machine Learning models and a set of dummy variables contains the exact same information as the original variable.
In modern Machine Learning jargon, creating dummies is also called one-hot-encoding.
You can create dummies using Pandas as follows:
The data will now contain three variables for the countries: one for each country. The values are 1 if the row belongs to this country and 0 otherwise:
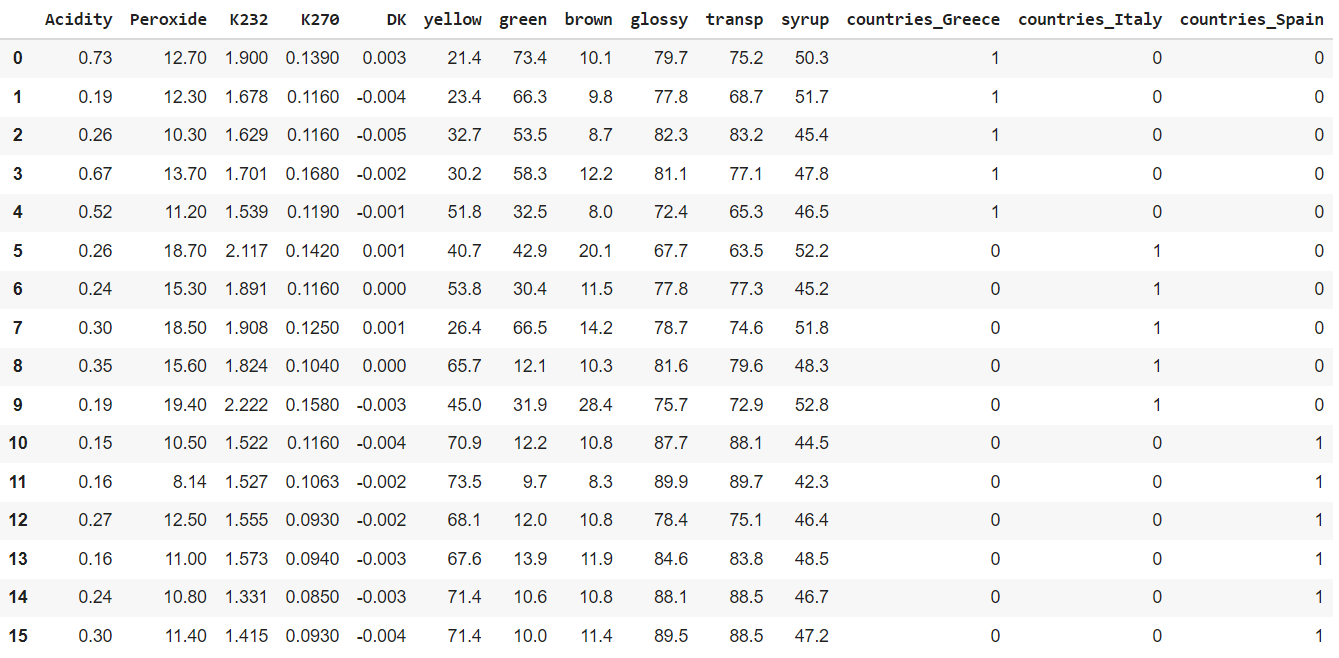
The next step is to split the data in an X data frame and a Y data frame, because this is required by the PLS model in Python:
Now we get to the model. We'll use the PLSRegression from the scikitlearn package. We can fit it directly with 2 components to give the same interpretation as we did in the R example.
The difficulty with multivariate statistics in Python is often the plot creation. In the following code block, a biplot is created. It is coded step by step:
- First we obtain the scores. Scores represent how high each individual olive oil scores on each dimension. The scores will allow us to plot the individuals in the biplot.
- We need to standardize the scores to make them fit on the same plot as the loadings.
- Then we obtain the loadings. The loadings contain the weights of each variable on each component. They will allow us to plot the variables on the biplot.
- We then loop through each individual and each variable and we plot an arrow and a label for them. The dimension 1 score or loading will become the x-coordinate on the plot and the dimension 2 score or loading will become the y-coordinate on the plot.
The code is shown here:
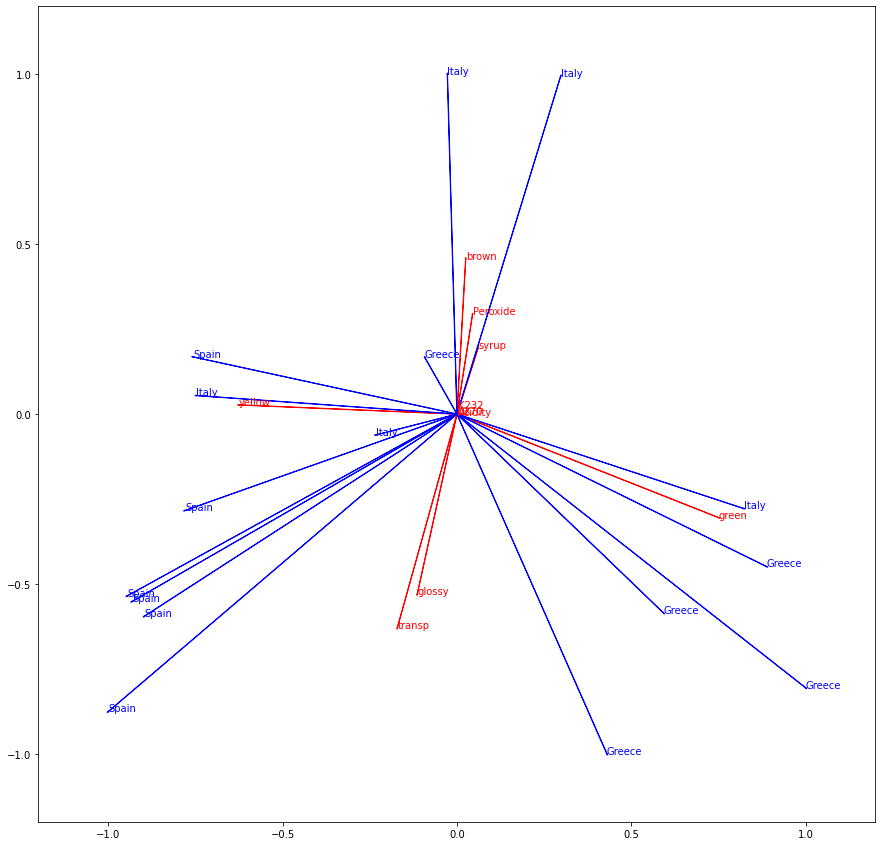
The resulting biplot is shown below:
Conclusion
The R interpretation of the biplot will give you the same findings as the Python biplot. To quickly recap the findings:
- Dimension 1 (x-axis) has green on one side and yellow on the other. The split between yellow and green oil is therefore important.
- On the green side, there are a lot of Greek oils and on the yellow side, there are a lot of Spanish oils. The green/yellow split allows differentiating Greek and Spanish olive oils.
- Dimension 2 (y-axis_ has brown on one side and glossy and transparent on the other side. Apparently, there is a split between oils that are either brown or else they are glossy and transparent, but not both at the same time.
- Italian oils tend to be on the brown side, whereas Spanish and Greek oils tend to be on the glossy and transparent side.
Key take-aways
In this article, you have first seen an overview of the (many) variants of Partial Least Squares that exist. Furthermore, you have seen in-depth explanations and implementations for two ways to use Partial least Squares:
- Partial Least Squares as a Machine Learning algorithm for predictive performance in the Meats example
- Partial Least Squares for interpretation in the olive oils example
You also have seen how to use Partial Least Squares with different types of dependent variables:
- Partial Least Squares Regression for the numeric dependent variables in the meats use case
- Partial Least Squares Discriminant Analysis for the categorical dependent variables in the olive oil use case
By using both R and Python implementations for both examples, you now have the needed resources to apply Partial Least Squares on your own use cases!
For now, thanks for reading and don't hesitate to stay tuned for more math, stats and data science content!
Graph These Data and Draw the Least Squares Line
Source: https://towardsdatascience.com/partial-least-squares-f4e6714452a
0 Response to "Graph These Data and Draw the Least Squares Line"
Enregistrer un commentaire